En aquest miniprojecte programaràs un joc d’ordinador. L’objectiu d’aquest exercici és portar la programació una mica més lluny i crear un petit videojoc on el nostre aguerrit heroi, el famós científic Newton, intenta no perdre l’oportunitat que la poma li caigui al cap.

Crearem, pas a pas, un programa en el qual Newton col·leccionarà punts durant mig minut en rebre tants cops de poma al cap com sigui possible.

1. Crea una poma i un científic

   Crea la pantalla del joc. Les pomes, per ara, seran cercles que cauen del cel i Newton serà un quadrat al fons de la pantalla.

   Noves ordres:

   • rect(x, y, width, height): Dibuixa un rectangle. x i y estableixen la posició de la cantonada superior esquerra; width i height n’estableixen la mida.

   

   De moment, Newton no es pot moure del centre de la finestra per agafar la poma, que està situada a la seva esquerra.

2. Pren el control de Newton amb el teclat

   Fes que Newton (el quadrat) es mogui amb les fletxes del teclat. Per accedir al teclat des de Processing, considera el següent: cada tecla del teclat té un keyCode. El keyCode és el valor o símbol que representa una tecla específica. keyCode és una variable de sistema interna que pot ser utilitzada per detectar quina tecla ha estat premuda. Per veure quina tecla ha estat premuda, utilitzarem una funció anomenada keyPressed(). Veurem que també necessitem una variable per guardar les coordenades de l’eix X (horitzontal) del quadrat, de manera que el puguem ajustar cada vegada que una tecla sigui premuda.

   Noves ordres:

   • keyPressed(): aquesta funció es crida cada vegada que una tecla és premuda. Això significa que qualsevol codi escrit dins d’aquesta funció serà executat en prémer una tecla.
   • keyCode: retorna el valor de la tecla que has premut.

   La variable nX s’utilitza per establir la posició x de Newton. Cada vegada que es prem el cursor dret, nX s’incrementa en 3 i cada vegada que es prem el cursor esquerra, nX decreix en 3. Ara ja pots moure el quadrat per la pantalla d’esquerra a dreta, però vigila, perquè pot sortir dels límits de la pantalla.

   

3. Limita els moviments del quadrat

   Limita el moviment de Newton dins de la finestra. Per fer-ho, utilitzaràs les funcions condicionals ‘if-else’, amb les quals comprovaràs que la coordenada X estigui sempre dins la finestra del programa. És a dir, haurà de ser major que 0 i menor que l’amplada de la finestra o width.

   En aquest cas, no veuràs gran diferència amb allò que es mostra a la pantalla del programa, amb l’excepció que el quadrat no sortirà dels seus límits.

4. Pomes que cauen

   Modifica el programa per fer que la poma (cercle) caigui des de dalt de la pantalla. Per fer-ho, necessitaràs una variable que contingui la coordenada Y del cercle i que, quan la poma toqui a terra, n’aparegui una altra a dalt.

   Hem creat una variable mY per emmagatzemar la coordenada Y de la poma. Cada vegada que draw() s’executa,  mY s’incrementa en 1, fent que la poma es vagi acostant al terra de la finestra. Quan la poma arriba a terra, és a dir, quan  mY és major que height, ha de reaparèixer màgicament dalt de la finestra.

   

5. Una mica d’atzar

   Fins ara, les pomes sempre surten de la mateixa posició des de dalt de la pantalla: així és bastant previsible. Per canviar la X d’origen i que cada vegada surti d’un lloc diferent de l’arbre, farem ús d’una funció anomenada random() que permet generar números aleatoris. Necessitaràs una nova variable per emmagatzemar la posició a X de la poma. Pensa que s’haurà de canviar la coordenada només quan la poma toqui a terra, perquè si no canviarà de posició aleatòriament durant la caiguda.

   Noves ordres:

   • random(high): genera un número aleatori entre 0 i el número high. Pots utilitzar també random(low,high) per generar un número entre low i high.

   Amb aquest canvi al programa, podràs veure que les pomes surten des de qualsevol punt de dalt de la pantalla.

   

6. Detecció de col·lisió

   Detecta que la poma aterra al cap de Newton per poder comptar punts. L’acció de detectar que dos objectes xoquen a la pantalla s’anomena detecció de col·lisió. Utilitza les funcions condicionals if-else per veure si el cercle està sobre el quadrat i que, quan sigui així, el color del quadrat es posi vermell. Per fer el programa més simple, crearem una variable que emmagatzemi les coordenades Y del quadrat i poder així fer les comparacions d’una manera més senzilla.

   Noves ordres:

   • if(test && test) {statements}: això s’utilitza quan vàries comprovacions han de ser realitzades en un únic if(). En aquest exemple, comprovarem si mY+10 > nY i si mY-10 < nY+20. Si aquestes dues comprovacions són certes alhora, executem el codi entre claus.

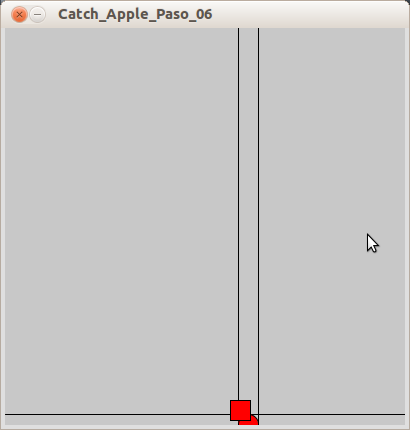
   La detecció de col·lisió consisteix en dos if(). El primer comprova si el cercle és a la mateixa alçada que el quadrat. Si és així, el segon if() comprova si el cercle és damunt del quadrat. Si és així, el fill() pinta el cercle de color vermell. Una col·lisió ha de ser semblant a això:

   

   D’altra banda, si actives les següents línies al programa:

   // lines of code to understand how collision works
   // erase the comment in order to see the code
   line(0,mY-10,width,mY-10);
   line(mX-10,0,mX-10,height);
   line(0,mY+10,width,mY+10);
   line(mX+10,0,mX+10,height);

   Veuràs una sèrie de línies a la pantalla emmarcant el moviment de la poma. Les pots fer servir per veure com funciona la detecció de col·lisió.

   

7. Més ràpidament

   Vols que les pomes caiguin més ràpidament? Modifica’n la velocitat per fer el joc una mica més interessant. Per fer-ho, crea una variable float perquè mV emmagatzemi la velocitat de caiguda de les pomes. Pots canviar la velocitat modificant el valor de mV. Al mateix temps, per poder controlar millor el moviment de la poma a l’eix Y, modificarem el tipus de variable de mY perquè sigui float. Recordes float de la secció de variables? Una variable amb dades del tipus float pot emmagatzemar números decimals.

   Enlloc d’incrementar 1 mY, l’incrementarem amb mV. Res ha canviat al programa a part de la velocitat: només hi ha una petita diferència entre aquest i el programa anterior.

8. A Newton li agrada la gravetat: dóna-li’n més

   Modifica la caiguda de les pomes perquè respongui a l’acceleració de la gravetat. D’aquesta manera, com més temps portin caient, més ràpid aniran les pomes. Com saps, la velocitat es calcula a partir de l’acceleració i, de la mateixa manera, la posició es calcula a partir de la velocitat. Per fer aquestes operacions de la manera més senzilla possible, introdueix una variable en coma flotant (float) que representi l’acceleració.

   Cada vegada que incrementis mY, incrementarem també una mica mV. D’aquesta manera, la velocitat serà una mica més gran cada vegada. A part de l’acceleració, res ha canviat al programa: només hi ha una petita diferència entre aquest i l’anterior.

9. Compta els punts

   Implementa un comptador que mostri quantes pomes han xocat amb Newton. Per mostrar el text, pots utilitzar la funció text(). A més a més, necessitaràs un comptador per anotar els punts.

   Nota: com que comences a tenir moltes variables al teu programa, és recomanable que afegeixis comentaris per recordar què fa cadascuna d’elles.

   Noves ordres:

   • text(test, x, y): escriu un text a la pantalla a les coordenades x i y.

   Hem declarat una nova variable p que s’incrementa en una unitat cada vegada que es detecta una col·lisió. L’última cosa que fem a draw() és mostrar el comptador dels punts a la cantonada superior dreta.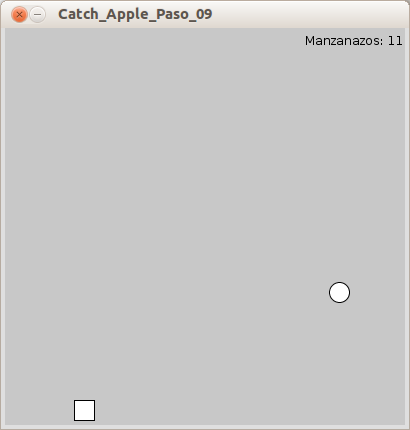

   

10. Ups! Error

    T’hauràs adonat que ara mateix el teu programa està comptabilitzant punts de més a més. Cada vegada que la poma cau sobre el cap de… eh… quan el cercle toca el quadrat, el teu comptador puja més o menys 5 punts. Per corregir això, tens dues opcions:

    • Torna a llançar la poma just quan es detecti la col·lisió.
    • Deixa de comptar quan hi hagi col·lisió, fins que es llanci una nova poma.

    Per evitar qualsevol d’aquestes dues possibilitats, necessites una variable de tipus boolean on emmagatzemar l’estat de la poma. Recordes què era una variable boolean? Podem utilitzar aquesta variable per dir-li al programa si comptar punts o no.

    Noves ordres:

    • if( boolean ): comprova si boolean és true. Pots també comprovar si és fals escrivint if( !boolean ).

    Ara prova el programa per veure com compta un únic punt per poma. Això succeeix perquè només afegim punts quan la variable boolean pCount és true i canvia a false just després de comptar el punt. Quan la poma és rellançada, pCount es torna a posar a true.

11. I el temps comença

    L’objectiu del joc és rebre tantes pomes com sigui possible en un període de temps determinat. Per poder comptabilitzar això, només necessitem un comptador de temps que també es mostri a la pantalla, a fi que els jugadors sàpiguen quan s’ha acabat la partida. La duració òptima del joc és de mig minut. Si és massa curt, no hi haurà manera d’aconseguir punts, mentre que si és massa llarg serà avorrit. Per mesurar el temps, pots utilitzar una funció anomenada millis() que comptabilitza els milisegons que han passat des de l’última vegada que se l’ha cridat. D’aquesta manera pots veure si han passat 30000 milisegons (30 segons) per acabar el joc. Per emmagatzemar el temps, necessites una variable del tipus long. La funció noLoop() li dirà al teu programa que acabi un cop hagis arribat al final. En darrer lloc, utilitza text() per mostrar el temps que queda a la pantalla.

    Noves ordres:

    • long: aquest és un tipus de dades per números enters llargs. Convé utilitzar-les quan fem servir variables temporals, perquè aquestes dades poden ser molt grans. Recordes que vam explicar que una variable és un contenidor de dades? Bé, es pot dir que long és un contenidor més gran que int. Un int es queda sense espai abans que un long.
    • noLoop(): atura l’execució contínua dins de draw. Per tornar a executar el programa hauràs de cridar a loop().

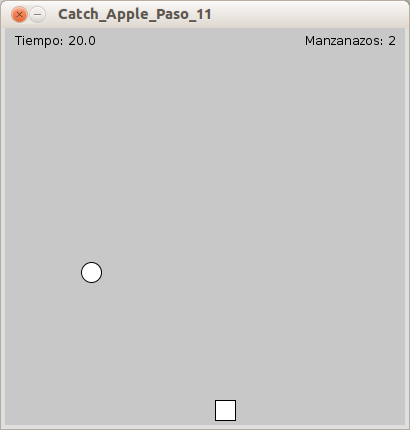
    La variable de temps t s’inicialitza al setup(). Com que millis() compta la quantitat de milisegons que el programa s’ha executat, t agafa un valor proper a 0. Per fer-ho més fàcil, direm que és igual a 0. Després d’haver dibuixat a Newton i la poma, crearem una nova variable anomenada timer que calcula quant temps ha passat. Això es fa amb (millis()-t)/1000. Quan han passat 10 segons, aquest càlcul serà: (10000-0)/1000.

    Si timer és major que 30, cridem a noLoop() per parar el programa. Com que timer no és més gran que 30, utilitza text()per mostrar quant temps queda.

    El joc amb comptador de temps es veurà de la següent manera:

    

12. Afegeix imatges al joc

    Inclou imatges per la poma, el fons i Newton. Les pots crear tu, buscar-les a Internet  o utilitzar les que et passem. És important que les imatges siguin de tipus PNG si vols que hi hagi transparència entre les imatges i el fons. Pensa que, quan canviïs les formes per imatges, les proporcions també canviaran, per la qual cosa hauràs d’encaixar aquests valors a la part del programa dedicat a la detecció de col·lisions.

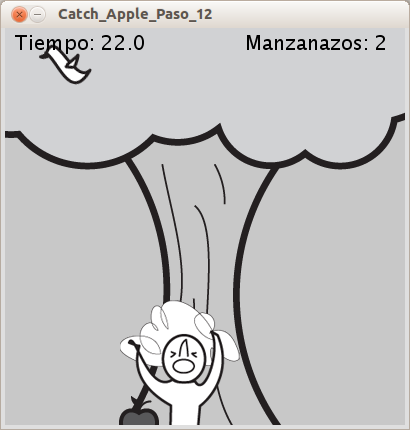
    Per pujar les imatges utilitzem el mateix mètode que als projectes anteriors, mitjançant arrays. Enlloc de canviar el color de les formes quan una col·lisió sigui detectada, utilitzem el boolean pCount per decidir quina imatge de Newton mostrar.

    El resultat final del joc es mostra de la següent manera:

    

Continua experimentant!

Per millorar aquest joc pots fer diverses coses:

• Fes les teves pròpies imatges.
• Crea una pantalla d’inici i que comenci el joc un cop es premi un botó.
• Crea una pantalla final que mostri el resultat un cop s’hagi acabat el temps.
• Fes possible reiniciar el joc quan el temps s’hagi acabat. No oblidis reiniciar totes les variables necessàries.
• Fes servir superpoders científics: fes que Newton es pugui moure amb acceleració i no només a velocitat constant.