En este mini proyecto programarás un juego de ordenador. El objetivo de este ejercicio es llevar la programación un poco más lejos y crear un pequeño videojuego donde nuestro aguerrido héroe, el famoso científico Newton, intenta no perder la oportunidad de que la manzana le caiga en la cabeza.

Vamos a crear, paso a paso, un programa en el que Newton coleccione puntos durante medio minuto, al recibir tantos manzanazos en la cabeza como sea posible.

1. Crea una manzana y un científico

   Crea la pantalla del juego. Las manzanas, por ahora, serán círculos que caen del cielo, mientras que Newton será un cuadrado al fondo de la pantalla.

   Nuevos comandos:

   • rect(x, y, width, height): Dibuja un rectángulo. x e y establecen la posición de la esquina superior izquierda, width y height establecen el tamaño.

   

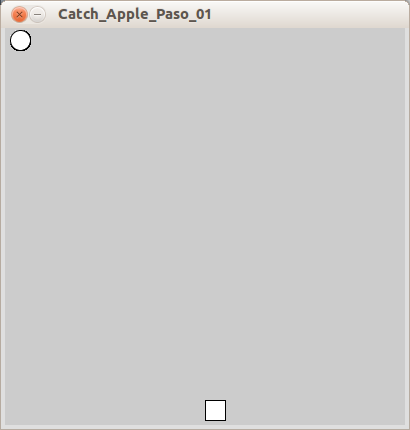
   De momento, Newton no se puede mover del centro de la ventana para coger la manzana, que está situada a su izquierda.

2. Toma el control de Newton con el teclado

   Haz que Newton (el cuadrado) se mueva con las flechas del teclado. Para acceder al teclado desde Processing, considera lo siguiente: cada tecla del teclado tiene un keyCode. El keyCode es el valor o símbolo que representa una tecla específica. keyCode es una variable de sistema interna que puede ser usada para detectar qué tecla ha sido pulsada. Para ver que tecla ha sido apretada, vamos a usar una función llamada keyPressed(). Veremos que también necesitamos una variable para guardar las coordenadas del eje X (horizontal) del cuadrado, de forma que lo podamos ajustar cada vez que una tecla sea pulsada.

   Nuevos comandos:

   • keyPressed(): esta función se llama cada vez que una tecla es pulsada. Esto significa que cualquier código escrito dentro de esta función será ejecutado al pulsar una tecla.
   • keyCode: devuelve el valor de la tecla que has pulsado.

   La variable nX se usa para establecer la posición x de Newton. Cada vez que se pulsa el cursor derecho, nX se incrementa con 3 y cada vez que se pulsa el cursor izquiero, nX se decrementa en 3. Ahora ya puedes mover el cuadrado por la pantalla de izquierda a derecha, pero ten cuidado, porque puede salirse de los límites de la pantalla.

   

3. Limita los movimientos del cuadrado

   Limita el movimiento de Newton dentro de la ventana. Para esto vas a usar las funciones condicionales ‘if-else‘, con las que comprobarás que la coordenada X esté siempre dentro de la ventana del programa. Es decir, tendrá que ser mayor que 0 y menor que la anchura de la ventana o width.

   En este caso, no hay una gran diferencia en lo que se verá en la pantalla del programa, con la excepción de que el cuadrado ya no se saldrá de los límites.

4. Manzanas que caen

   Modifica el programa para hacer que la manzana (círculo) caiga de lo alto de la pantalla. Para esto, necesitarás una variable que contenga la coordenada Y del círculo y, cuando la manzana toque el suelo, que aparezca otra arriba.

   Hemos creado una variable mY para almacenar la coordenada Y de la manzana. Cada vez que draw() se ejecuta, mY se incrementa en 1, haciendo que la manzana vaya acercándose al suelo de la ventana. Una vez que la manzana llega al suelo, es decir, mY es mayor que height, debe reaparecer mágicamente en lo alto de la ventana.

   

5. Un poco de azar

   Hasta ahora, las manzanas siempre salen de la misma posición en lo alto de la pantalla, así es bastante predecible. Para cambiar la X de origen y que cada vez salga de un sitio distinto del árbol, haremos uso de una función llamada random() que permite generar números aleatorios. Necesitarás una nueva variable para almacenar la posición en X de la manzana. Ten en cuenta que la coordenada habrá que cambiarla solo cuando la manzana llegue al suelo, porque si no cambiará aleatoriamente durante su caída.

   Nuevos comandos:

   • random(high): genera un número aleatorio entre 0 y el número high. Puedes también usar random(low,high) para generar un número entre low y high.

   Con este cambio en el programa, podrás ver que las manzanas salen desde cualquier punto en lo alto de la pantalla.

   

6. Detección de colisión

   Detecta que la manzana aterriza en la cabeza de Newton para poder contar puntos; la acción de detectar que dos objetos se chocan en la pantalla se llama detección de colisión. Utiliza las funciones condicionales if-else para ver si el círculo está sobre el cuadrado y, de ser así, cambia el color del cuadro a rojo. Para hacer el programa más sencillo, crearemos una variable que almacene las coordenadas Y del cuadrado, y así poder hacer las comparaciones de un modo más sencillo.

   Nuevos comandos:

   • if(test && test) {statements}: esto se utiliza cuando varias comprobaciones deben ser realizadas en un único if(). En este ejemplo, comprobamos si mY+10 > nY y si mY-10 < nY+20. Si estas dos comprobaciones son ciertas simultáneamente, ejecutamos el código entre llaves.

   La detección de colisión consiste en dos if(), el primero comprueba si el círculo está a la misma altura que el cuadrado. Si es así, el segundo if() comprueba si el círculo está arriba del cuadrado. De ser así, el fill() colorea el círculo en rojo. Una colisión debe ser similar a esto: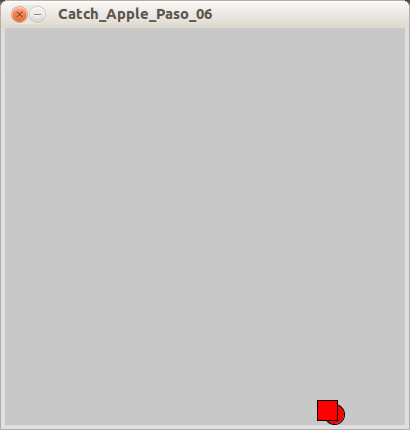

   

   Por otra parte, si activas las siguientes líneas en el programa:

   // lines of code to understand how collision works
   // erase the comment in order to see the code
   line(0,mY-10,width,mY-10);
   line(mX-10,0,mX-10,height);
   line(0,mY+10,width,mY+10);
   line(mX+10,0,mX+10,height);

   Verás una serie de líneas en la pantalla enmarcando el movimiento de la manzana. Puedes emplearlas para ver cómo funciona la detección de colisión.

   

7. Más rápido

   ¿No quieres que las manzanas caigan más rápido? Modifica la velocidad de las manzanas para hacer el juego algo más interesante. Para ello, crea una variable float para que mV almacene la velocidad de caída de la manzana. Puedes cambiar la velocidad modificando el valor de mV. Al mismo tiempo, para poder controlar mejor el movimiento de la manzana en el eje Y, vamos a modificar el tipo de variable de mY para que sea float. ¿Recuerdas float de la sección de variables? Una variable con datos del tipo float puede almacenar números decimales.

   En lugar de incrementar mY en uno, vamos a incrementarlo con mV. A parte de la velocidad, nada ha cambiado en el programa, por lo que sólo hay una pequeña diferencia entre este y el programa anterior.

8. A Newton le gusta la gravedad, dale más

   Modifica la caída de las manzanas para que responda a la aceleración de la gravedad. De este modo, las manzanas irán cada vez más rápido cuanto más tiempo lleven cayendo. Como sabes, la velocidad se calcula a partir de la aceleración, y del mismo modo, la posición a partir de la velocidad. Para hacer estas operaciones de la forma más sencilla posible, introduce una variable en coma flotante (float) que represente la aceleración.

   Cada vez que incrementes mY incrementaremos también mV un poco. De esta manera, la velocidad será un poco más grande cada vez. A parte de la aceleración, nada ha cambiado en el programa, por lo que sólo hay una pequeña diferencia entre este programa y el anterior.

9. Cuenta los puntos

   Implementa un contador que muestre cuántas manzanas golpearon a Newton. Para mostrar el texto, puedes utilizar la función text(). Además, necesitarás un contador para anotar los puntos.

   Nota: como empiezas a tener muchas variables en tu programa, es recomendable que añadas comentarios para recordar qué hace cada una.

   Nuevos comandos:

   • text(text, x, y): escribe un texto en la pantalla en las coordenadas x e y.

   Hemos declarado una nueva variable p que se incrementa en una unidad cada vez que se detecta una colisión. La última cosa que hacemos en draw() es mostrar el contador de los puntos en la esquina superior derecha.

   

10. Uoops, error

    Te habrás dado cuenta que tu programa ahora mismo está contabilizando puntos de más. Cada vez que la manzana cae sobre la cabeza de Newton… eh… cuando el círculo toca el cuadrado, tu contador sube más o menos 5 puntos. Para corregir esto tienes un par de opciones:

    • Vuelve a lanzar la manzana en cuanto se detecte colisión.
    • Deja de contar cuando haya colisión, hasta que se lance una nueva manzana.

    Para evitar cualquiera de estas dos posibilidades, necesitas una variable de tipo boolean donde almacenar el estado de la manzana. ¿Recuerdas qué era una variable boolean? Podemos usar esta variable para decirle al programa si contar puntos o no.

    Nuevos comandos:

    • if( boolean ): comprueba si boolean es true. Puedes también comprobar si es falso escribiendo if( !boolean ).

    Ahora prueba el programa para ver cómo cuenta un único punto por manzana. Esto es porque sólo añadimos puntos cuando la variable boolean pCount es true y cambia a false justo después de contar el punto. Cuando la manzana es relanzada, pCount se vuelve a poner en true.

11. Y el tiempo empieza

    El objetivo del juego es recibir tantas manzanas como sea posible en un periodo de tiempo determinado. Para poder contabilizar esto, sólo necesitamos un contador de tiempo, que también se muestre en la pantalla, para que los jugadores sepan cuándo ha terminado la partida. La duración óptima del juego es de medio minuto, si es demasiado corto, no habrá forma de conseguir puntos mientras que, si es demasiado largo, se hará aburrido. Para medir el tiempo, puedes usar una función llamada millis() que contabiliza los milisegundos que han pasado desde la última vez que se le llamó. De este modo puedes ver si han pasado 30000 milisegundos (30 segundos) para terminar el juego. Para almacenar el tiempo, necesitas una variable de tipo long. La función noLoop() le dirá a tu programa que termine una vez hayas llegado al final del mismo. Finalmente, usa text() para mostrar el tiempo que queda en la pantalla.

    Nuevos comandos:

    • long: este es un tipo de datos para números enteros largos. Es conveniente usarlos cuando manejamos variables temporales, porque estos datos pueden ser muy grandes. ¿Recuerdas cómo explicamos que una variables es un contenedor de datos? Bien, se puede decir que long es un contenedor más grande que int. Un int se queda sin espacio antes que un long.
    • noLoop(): detiene la ejecución continua dentro de draw. Para volver a ejecutar el programa tendrás que llamar a loop().

    La variable de tiempo t se inicializa en el setup(). Puesto que millis()cuenta la cantidad de milisegundos que el programa se ha ejecutado, t tomará un valor cercano a 0. Digamos que, para hacerlo más fácil, es igual a 0. Después de haber dibujado a Newton y la manzana, creamos una nueva variable llamada timer que calcula cuanto tiempo ha pasado. Esto se hace con (millis()-t)/1000. Cuando han pasado 10 segundos, este cálculo sería: (10000-0)/1000.

    Si timer es mayor que 30, llamamos a noLoop() para parar el programa. Pero puesto que timer no es mayor que 30, utiliza text()para mostrar cuanto tiempo queda.

    El juego con contador de tiempo se verá como sigue:

    

12. Añade imágenes al juego

    Incluye imágenes para la manzana, el fondo y Newton. Las puedes crear tú, buscarlas en Internet, o usar las que te pasamos. Es importante que las imágenes sean de tipo PNG si quieres que haya transparencia entre las imágenes y el fondo. Ten en cuenta que, al cambiar las formas por imágenes, las proporciones también cambian, por lo que tendrás que hacer encajar esos valores en la parte del programa dedicado a la detección de colisiones.

    Para cargar las imágenes utilizamos el mismo método que en los proyectos anteriores, utilizando arrays. En lugar de cambiar el color de las formas cuando una colisión sea detectada, utilizamos el boolean pCount para decidir qué imagen de Newton mostrar.

    El resultado final del juego se ve como sigue:

    

¡Sigue experimentando!

Para mejorar este juego puedes hacer varias cosas:

• Haz tus propias imágenes.
• Crea una pantalla de inicio y que se pase al juego una vez se presione un botón.
• Crea una pantalla final que muestre el resultado una vez se haya terminado el tiempo.
• Haz posible reiniciar el juego cuando el tiempo haya terminado. No te olvides de reiniciar todas las variables necesarias.
• Usa superpoderes científicos, haz que Newton se pueda mover con aceleración y no solo a velocidad constante.